

We’re going to go 90 degrees and everything in this quadrant has a negative x value and a positive Y value. Counterclockwise is in this direction so it spins counter to the way the hands of a clock spin.
Here is figure ABCD, we have to rotate it 90 degrees counterclockwise. Number two on our rotation rules for math worksheet tells us to rotate figure ABCD 90 degrees counterclockwise.

And then if you rotate it again the X and the y would flip-flop again, from one to two to one and then everything in quadrant two has a negative x value. It would rotate back but this time everything in this quadrant is negative negative so this would be negative one and this would be negative two and you’d plot it here. It’s two negative one and then if we wanted to rotate again one will become one two. The two is positive and the y is negative and then you can plot your new point.

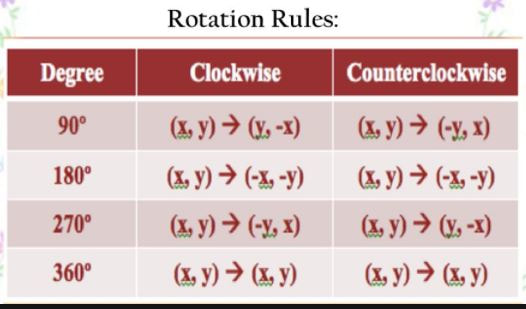
Then our coordinate has to match that of the quadrant, which in this case is positive negative. If we start here at 1, 2 and we rotate 90 degrees into quadrant four, the one and the two will become two one. The last rotation rule that you must know is that every time you rotate 90 degrees in either direction clockwise or counter clockwise you flip-flop the x and the y value. So in this case our coordinate is to two our x value will be negative because we’re in the second quadrant and the y value will be positive. This is important to know because as you rotate around the origin and you end up in a different quadrant, the coordinates on your point will always match the coordinates of the quadrant. Every single coordinate in quadrant one will have a positive x value and a positive Y value, every single coordinate in quadrant two will have a negative x value and a positive Y value, quadrant three every single coordinate is negative negative, and then quadrant four every single coordinate is positive x and a negative Y. This is quadrant one, quadrant two, quadrant three, and finally quadrant four. The quadrants are labeled in a counterclockwise rotation around the origin. The next rotation rule has to do with the quadrants.
Clockwise rotation rules full#
Our next quadrant would be 90 more degrees and then 270 degrees total, and then of course if you went back to the original spot it would be 360 degrees or a full rotation around the origin. If we go this way, it’s still 90 and then if we go one more quadrant it’s 90 more again, and then 180 total. The same rotation rules would apply when going in the counterclockwise direction. You can do the same thing in the opposite direction.
Clockwise rotation rules plus#
In this case we’re going clockwise and then if we went 90 more degrees, or if we want one more quadrant, it would be 90 more degrees and then total it would be 90 plus 90 plus 90 or 270 degrees total rotation. If we rotate it again it would be 90 more degrees or total from this point to this point would be 90 plus 90 or 180 degrees total. If we rotate one quadrant either clockwise or counter clockwise that would be a 90 degree rotation. You could also take a and rotate it counterclockwise which would go in this direction, and then a prime would be over here.Īnother rotation rule is that you have to know that the degree measures of rotation are all in 90 degrees. This would be a 90-degree rotation clockwise. It would rotate this way and it would become a prime down here. If we had a here and we wanted to rotate it clockwise.


 0 kommentar(er)
0 kommentar(er)
